The number of square feet per house are normally distributed with a population standard deviation of 137 square feet and an unknown population mean. A random sample of 19 houses is taken and results in a sample mean of 1350 square feet.
Find the margin of error for a 80% confidence interval for the population mean.
![]()
You may use a calculator or the common z values above.
- Round the final answer to two decimal places.
QUESTION 2
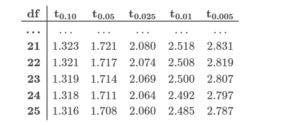
The speeds of vehicles traveling on a highway are normally distributed with an unknown population mean and standard deviation. A random sample of 11 vehicles is taken and results in a sample mean of 65 miles per hour and sample standard deviation of 9 miles per hour.
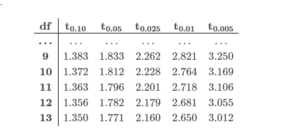
Eric wants to estimate the percentage of elementary school children who have a social media account. He surveys 450 elementary school children and finds that 280 have a social media account.
Identify the values needed to calculate a confidence interval at the 99% confidence level. Then find the confidence interval.
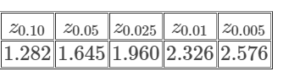
Use the table of common z-scores above.
- Round the final answer to three decimal places.
Use the Empirical Rule to construct a 95% confidence interval for the true proportion of adults who prefer e-books.
QUESTION 6
Which of the following results in the null hypothesis μ=38 and alternative hypothesis μ<38?
QUESTION 7
The answer choices below represent different hypothesis tests. Which of the choices are left-tailed tests? Select all correct answers.

According to a survey, the average American person watches TV for 3 hours per week. To test if the amount of TV in New York City is less than the national average, a researcher decides to do a hypothesis test, at a 1% significance level. She surveys 19 New Yorkers randomly and asks them about their amount of TV each week, on average. From the data, the sample mean time is 2.5 hours per week, and the sample standard deviation (s) is 0.9 hours.
- H0: μ≤3; Ha: μ>3.
- α=0.01 (significance level)
What is the test statistic (t-value) of this one-mean hypothesis test (with σ unknown)?
- Round your final answer to two decimal places.
- QUESTION 10
A teacher claims that the proportion of students expected to pass an exam is greater than 80%. To test this claim, the teacher administers the test to 200 random students and determines that 151 students pass the exam.
The following is the setup for this hypothesis test:
{H0:p=0.80Ha:p>0.80Find the test statistic for this hypothesis test for a proportion. Round your answer to 2 decimal places.
QUESTION 11·Based on the following results, conclude whether to reject or not reject H0.
- H0 : p=0.75; Ha : p>0.75
- α=0.05 (significance level)
- The test statistic is 2.59.
- The critical value is z0.05=1.65.
Select two responses below.
QUESTION 12·Stephanie, a physician, would like to make the claim that her patients get less than 180 minutes of exercise per week, on average. Another physician who works at the same office doesn’t believe her, so Stephanie decides to do a hypothesis test. She samples 25 patients, obtains a sample average of 179.1 minutes, and works through the testing procedure:
- H0: μ=180; Ha: μ<180
- α = 0.05 (significance level)
- The test statistic is t0=x¯−μ0sn√=179.1−1802.125√=−2.143.
- The degrees of freedom is 24, and the critical value is −t0.05=−1.711.
Conclude whether to reject or not reject H0. Select two responses below.
QUESTION 13·Suppose the manager of a shoe store wants to determine the current percentage of customers who are males. How many customers should the manager survey in order to be 98% confident that the estimated (sample) proportion is within 8 percentage points of the true population proportion of customers who are males?
 QUESTION 14·
QUESTION 14·The lengths of text messages are normally distributed with a population standard deviation of 3 characters and an unknown population mean. If a random sample of 29 text messages is taken and results in a sample mean of 25 characters, find a 98% confidence interval for the population mean. Round your answers to two decimal places

The population standard deviation for the heights of dogs, in inches, in a city is 4.9 inches. If we want to be 80% confident that the sample mean is within 1 inch of the true population mean, what is the minimum sample size that can be taken?

Solution:

……..Click link below to purchase full tutorial at $15