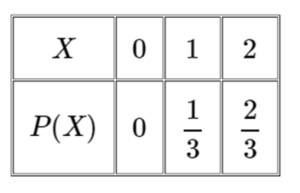
Question
For a certain animal, suppose that the number of babies born is independent for each pregnancy. This animal has a 70% chance of having 1 baby and a 30% chance of having 2 babies at each pregnancy. Let X be a random variable that represents the total number of babies if the animal gets pregnant twice. Construct a table showing the probability distribution of X. Arrange x in increasing order.
- Write the probabilities P(x)as decimals rounded to two decimals.
Question
Oliver is a quality control manager in the electrical switches department of a manufacturing plant. If Oliver randomly selects 200 switches for a check of a recently produced lot, the probability of selecting exactly 1 defective switch is 0.360, the probability of selecting exactly 2 defective switches is 0.144, the probability of selecting exactly 3 defective switches is 0.038, the probability of selecting exactly 4 defective switches is 0.008, and the probability of selecting exactly 5 defective switches is 0.001. Let X denote the number of defective switches Oliver selects. Assuming the probability of Oliver selecting 6 or more defective switches is 0, construct the probability distribution of X. Write the probabilities as decimals.
Question
Determine whether or not the distribution is a probability distribution and select the reason(s) why or why not.
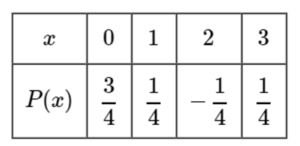
Correct answer:
The given distribution is not a probability distribution, since at least one of the probabilities is greater than 1 or less than 0.
Question
A news program reports that 37% of the population are in favor of a certain issue, 42% are against the issue, and the rest are undecided. Let X be the preference of one person randomly selected from the population.
Complete the corresponding probability distribution table.
Answer:
Question
Determine whether or not the distribution is a probability distribution and select the reason(s) why or why not.
The given distribution is a probability distribution, since the probabilities lie inclusively between 0 and 1.
Question
Which of the following events seem like they would be unlikely to occur by chance? Select all that apply.
Question
A hospital takes record of any birth that occurs there every day. On one day, the hospital reports that 35 of the 62 babies born were girls. Assuming that all of the parents did not have any gender selection procedures, there is a probability of 0.31 of getting these results by chance. Do these results have statistical significance at the 0.05 level of significance?
Question
A flood insurance company sells policies for $700 per year. If a customer’s house is flooded, they are given $250,000 for repairs. The insurance company has calculated the chances that a house is flooded to be 1/ 12,500 over the year. How much money can the insurance company expect to make with each policy sold?
- Round your answer to the nearest cent.
- Enter an expected loss as a negative number.
Question
Suppose you play a game where you toss three fair coins. If you get three tails, you win $10. Otherwise, you lose $2. If you were to play this game 15 times, how much would you expect to gain or lose?
- Do not round until the final answer.
- Enter an expected loss as a negative number.
Question
A standard roulette wheel with slots labeled 0, 00, 1, 2, 3, … , 36 is spun 60 times. Of these spins, the number 7 is spun 7 times. Assuming the wheel is fair, the probability of this occurring by chance is 0.00001. Do these results have statistical significance at the 0.01 level of significance?
Question
A farmer claims that the average mass of an apple grown in his orchard is 100g. To test this claim, he measures the mass of 150 apples that are grown in his orchard and determines the average mass per apple to be 98g. The results are calculated to be statistically significant at the 0.01 level. What is the correct interpretation of this calculation?
Question
A news program reports that 52% of the population are in favor of a certain issue, 38% are against the issue, and the rest are undecided. Let X be the preference of one person randomly selected from the population.
Complete the corresponding probability distribution table.
Question
There are eight players on a basketball team. They are practicing their free throws by having each player shoot two free throws. The table below shows the results of each player’s free throw attempts, where N represents a missed free throw and Y represents a made free throw. Construct the probability distribution of X for the number of free throws made by the players. Arrange x in increasing order and write the probabilities P(x) as simplified fractions.

Question
You toss a coin three times. If you toss heads exactly two times, you win $2. If you toss heads all three times, you win $8. Otherwise, you lose $3. What is the expected payout for one round of this game?
- Round your answer to the nearest cent.
- Enter an expected loss as a negative number.
Question
You bet $50 on 00 in a game of roulette. If the wheel spins 00, you have a net win of $1,750, otherwise you lose the $50. A standard roulette wheel has 38 slots numbered 00, 0, 1, 2, … , 36. What is the expected profit for one spin of the roulette wheel with this bet?
- Round your answer to the nearest cent.
- Enter an expected loss as a negative number.
Question
A poll was conducted to determine if there was any possible connection between men and women who live in a certain city and the favorability of a mayor in the city. In the poll, of the 400 men selected, 210 reported being in favor of the mayor. Of the 400 women selected, 190 also reported being in favor of the mayor. The probability of these results occurring by chance is calculated to be about 0.16. Interpret the results of the calculation at the 0.05 level of significance.
Solution:
Question
For a certain animal, suppose that the number of babies born is independent for each pregnancy. This animal has a 70% chance of having 1 baby and a 30% chance of having 2 babies at each pregnancy. Let X be a random variable that represents the total number of babies if the animal gets pregnant twice. Construct a table showing the probability distribution of X. Arrange x in increasing order.
- Write the probabilities P(x)as decimals rounded to two decimals.
Answer:

Question
Oliver is a quality control manager in the electrical switches department of a manufacturing plant. If Oliver randomly selects 200 switches for a check of a recently produced lot, the probability of selecting exactly 1 defective switch is 0.360, the probability of selecting exactly 2 defective switches is 0.144, the probability of selecting exactly 3 defective switches is 0.038, the probability of selecting exactly 4 defective switches is 0.008, and the probability of selecting exactly 5 defective switches is 0.001. Let X denote the number of defective switches Oliver selects. Assuming the probability of Oliver selecting 6 or more defective switches is 0, construct the probability distribution of X. Write the probabilities as decimals.
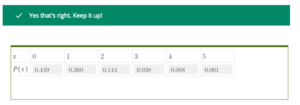
………Click link below to purchase full tutorial at $10