Question
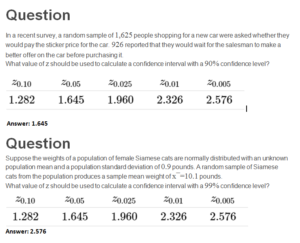
In a recent survey, a random sample of 1,625 people shopping for a new car were asked whether they would pay the sticker price for the car. 926 reported that they would wait for the salesman to make a better offer on the car before purchasing it.
What value of z should be used to calculate a confidence interval with a 90% confidence level?

Question
Suppose the weights of a population of female Siamese cats are normally distributed with an unknown population mean and a population standard deviation of 0.9 pounds. A random sample of Siamese cats from the population produces a sample mean weight of x¯=10.1 pounds.
What value of z should be used to calculate a confidence interval with a 99% confidence level?

Question
Suppose the number of snow days from a population of schools are normally distributed with an unknown population mean and a population standard deviation of 1.2 days. A random sample of schools from the population produces a sample mean of x¯=12.3 days.
What value of z should be used to calculate a confidence interval with a 95% confidence level?

Question
Suppose the weights of a population of female Bernese mountain dogs are normally distributed with an unknown population mean and a population standard deviation of 0.6 pounds. A random sample of Bernese mountain dogs from the population produces a sample mean weight of x¯=89.3 pounds.
What value of z should be used to calculate a confidence interval with a 99% confidence level?

Question
In a recent survey, a random sample of 190 third year law students were asked about their future employment. 49 reported that they had already secured a job for after graduation.
What value of z should be used to calculate a confidence interval with an 80% confidence level?
Question
Suppose the germination periods, in days, for grass seed are normally distributed. If the population standard deviation is 3 days, what minimum sample size is needed to be 90% confident that the sample mean is within 1 day of the true population mean?
Question
Suppose the finishing times for cyclists in a race are normally distributed. If the population standard deviation is 16 minutes, what minimum sample size is needed to be 95% confident that the sample mean is within 5 minutes of the true population mean?
Question
The population standard deviation for the scores of a standardized test is 5 points. If we want to be 95% confident that the sample mean is within 2 points of the true population mean, what is the minimum sample size that should be taken?
Question
The salaries of top executives at public companies are normally distributed with a population standard deviation of 17 thousand dollars and an unknown population mean. A random sample of 27 executives is taken and results in a sample mean of 319 thousand dollars.
Find the margin of error for a 95% confidence interval for the population mean.
Question
The lengths, in inches, of adult corn snakes are normally distributed with a population standard deviation of 6 inches and an unknown population mean. If a random sample of 18 snakes is taken and results in a sample mean of 61 inches, find the margin of error (ME) of the confidence interval with a 90% confidence level. Round your answer to three decimal places.
Answer: 2.326
Question
The number of hours that a nine month old baby sleeps at night are normally distributed with a population standard deviation of 1.5 hours and an unknown population mean. A random sample of 22 nine month old babies is taken and results in a sample mean of 12 hours.
Find the margin of error for a confidence interval for the population mean with a 90% confidence level.
Question
Suppose the speeds of vehicles traveling on a highway are normally distributed and have a known population standard deviation of 7 miles per hour and an unknown population mean. A random sample of 32 vehicles is taken and gives a sample mean of 64 miles per hour.
Find the margin of error for the confidence interval for the population mean with a 98% confidence level.
You may use a calculator or the common z values above.
- Round the final answer to two decimal places.
Question
Suppose the heights of a population of male giraffes are normally distributed with an unknown population mean and a population standard deviation of 3.4 feet. A random sample of male giraffes from the population produces a sample mean height of x¯=15.2 feet.
What value of z should be used to calculate a confidence interval with a 90% confidence level?
Question
In a recent survey, a random sample of 130 families were asked about whether they have a pet, and 67 reported that they have a pet.
What value of z should be used to calculate a confidence interval with a 90% confidence level?
Question
The heights of dogs, in inches, in a city are normally distributed with a population standard deviation of 7 inches and an unknown population mean. If a random sample of 20 dogs is taken and results in a sample mean of 21 inches, find a 95% confidence interval for the population mean.
Question
Suppose heights of seasonal pine saplings are normally distributed and have a known population standard deviation of 17 millimeters and an unknown population mean. A random sample of 15 saplings is taken and gives a sample mean of 308 millimeters.
Find the confidence interval for the population mean with a 90% confidence level.
Question
Suppose the number of free throws in a basketball game by one player are normally distributed with a standard deviation 0.97 free throws. A random sample of basketball players from the population produces a sample mean of x¯=4.9 free throws.
What value of z should be used to calculate a confidence interval with a 95% confidence level?
Question
A bank offers auto loans to qualified customers. The amount of the loans are normally distributed and have a known population standard deviation of 4 thousand dollars and an unknown population mean. A random sample of 22 loans is taken and gives a sample mean of 42 thousand dollars.
Find the margin of error for the confidence interval for the population mean with a 90% confidence level.
Question
The population standard deviation for the total snowfalls per year in a city is 13 inches. If we want to be 95% confident that the sample mean is within 3 inches of the true population mean, what is the minimum sample size that should be taken?
Answer:
Question
Suppose the number of defects in a sweater from a population of sweaters produced from a textile factory are normally distributed with an unknown population mean and a population standard deviation of 0.06 defects. A random sample of sweaters from the population produces a sample mean of x¯=1.3 defects.
What value of z should be used to calculate a confidence interval with a 95% confidence level?
Answer: 1.960
Question
The lengths, in inches, of adult corn snakes are normally distributed with a population standard deviation of 8 inches and an unknown population mean. A random sample of 25 snakes is taken and results in a sample mean of 58 inches.
What is the correct interpretation of the confidence interval?
Question
The lengths, in inches, of adult corn snakes are normally distributed with a population standard deviation of 8 inches and an unknown population mean. A random sample of 25 snakes is taken and results in a sample mean of 58 inches.
Identify the parameters needed to calculate a confidence interval at the 99% confidence level. Then find the confidence interval.
Question
The weekly salaries of sociologists in the United States are normally distributed and have a known population standard deviation of 425 dollars and an unknown population mean. A random sample of 22 sociologists is taken and gives a sample mean of 1520 dollars.
Find the margin of error for the confidence interval for the population mean with a 98% confidence level.
Question
Suppose the number of dollars spent per week on groceries is normally distributed. If the population standard deviation is 7 dollars, what minimum sample size is needed to be 90% confident that the sample mean is within 3 dollars of the true population mean?
Solution:
….Click link below to purchase full tutorial at $10